Turbine cascade

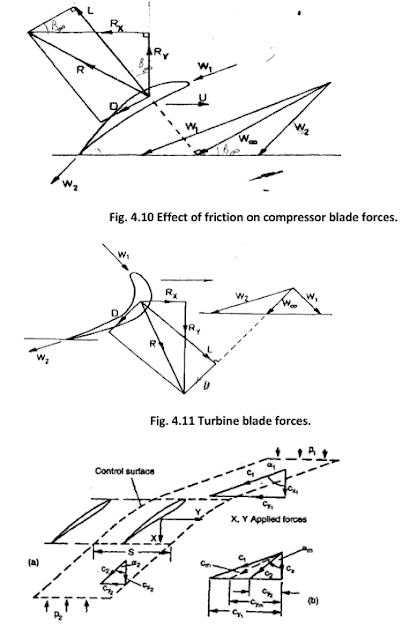
 TWO-DIMENSIONAL CASCADES

• What is turbine cascade? 
• What is cascade effect in gas turbine engine? 
• What are the three types of turbine blades? 
• What is turbine and its function?

•        The operation of any turbomachine is directly dependent upon changes in the working fluid’s angular momentum as it crosses individual blade rows.

•        A deeper insight of turbomachinery mechanics may be gained from consideration of the flow changes and forces exerted within these individual blade rows.

•        The range of Mach number in axial-flow turbomachines can be considered to extend from M = 0.2 to 2.5 (of course, if we also include fans then the lower end of the range is very low).

Two main types of cascade tunnel are:

(i) low-speed, operating in the range 20-60 m/s (ii) high-speed, for the compressible flow range of testing.

turbine cascade meaning

Conventional low-speed compressor cascade wind tunnels

 

•        To obtain truly two-dimensional flow would require a cascade of infinite extent. Of necessity cascades must be limited in size, and careful design is needed to ensure that at least the central regions (where flow measurements are made) operate with approximately two-dimensional flow.

•        A suction slot is situated on the ceiling of the tunnel just before the cascade to allow the controlled removal of the tunnel boundary layer.

Carefully controlled suction is usually provided on the tunnel sidewalls immediately upstream of the cascade so that two-dimensional, constant axial velocity flow can be achieved.

•        For axial flow machines of high hub—tip ratio (short blade), radial velocities are negligible and, to a close approximation, the flow may be described as two-dimensional.

•        The flow in a cascade is then a reasonable model of the flow in the machine.

•        With lower hub-tip radius ratios (long blade), the blades of a turbomachine will normally have an appreciable amount of twist along their length, the amount depending upon the sort of “vortex design” chosen. However, data obtained from two-dimensional cascades can still be of value to a designer requiring the performance at discrete blade sections of such blade rows.

  FIG. 3.15. Compressor cascade blade surf velocity distribution.

 

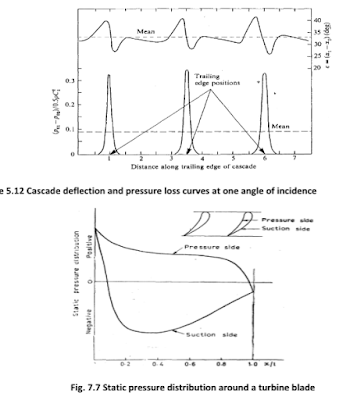
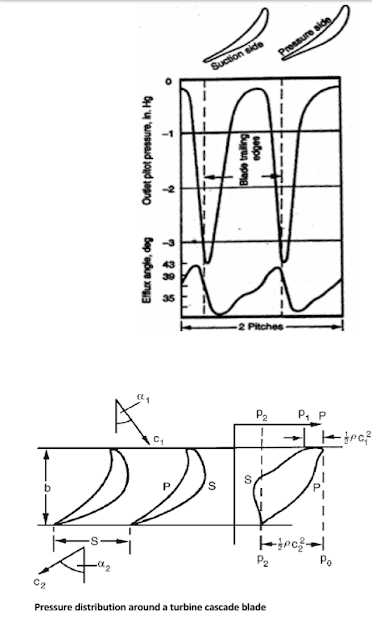
  Pressure distribution around a turbine cascade blade

Turbine cascade performance

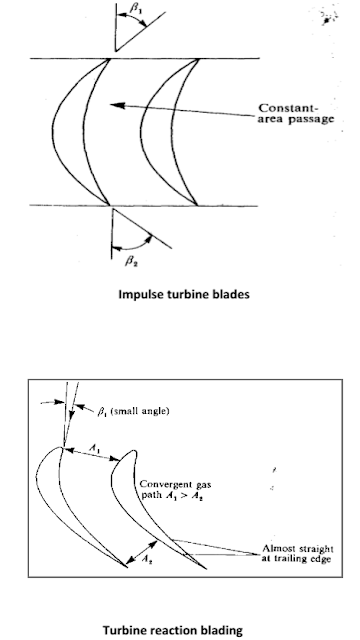
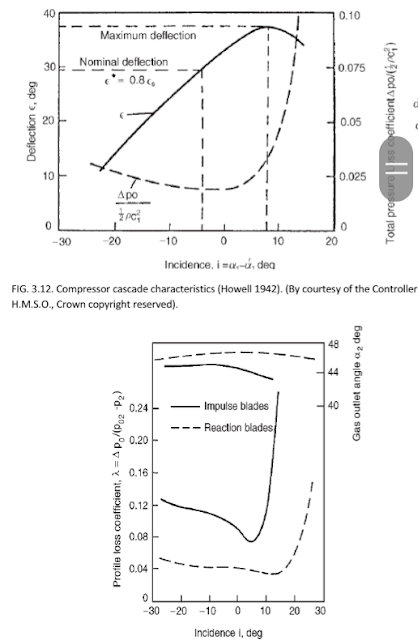
Figure 3.14 shows results obtained by Ainley (1948) from two sets of turbine cascade blades, impulse and “reaction”. The term “reaction” is used here to denote, in a qualitative sense, that the fluid accelerates through the blade row and thus experiences a pressure drop during its passage. There is no pressure change across an impulse blade row. The performance is expressed in the form                 ʎ= Δpo/(po2 -p2) and     ∝^2     against incidence.

From these results it is observed that:

(a)    the reaction blades have a much wider range of low loss performance than the impulse blades, a result to be expected as the blade boundary layers are subjected to a favorable pressure gradient,

(b) the fluid outlet angle 2 remains relatively constant over the whole range of incidence in contrast with the compressor cascade results.

FI. 3.13. Losses in a compressor stage (Howell 1945).

 

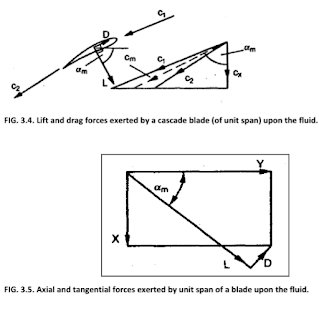
Two important geometric variables, which define blade shape are

•        Blade thickness distribution, t/l, and

•        Blade camber line shape distributions y/l, which may be circular or parabolic arce form or any other form. It determines the blade camber angle, θ.

•        Blade camber and thickness distributions are generally presented as tables of y/l and t/l against x / l. 

Beside the blade profile (thickness&camber distributions) there are two important geometric variables, which define the cascade are

•        the space-chord ratio, s/l, and

•        the stagger angle,Ƹ,

The stagger angle,ξ,

   is the angle between the chord line and the reference direction (which is the tangent to or the line perpendicular to the cascade front).

 

The importance of the stagger angle, x,

It affects the following:

   1- the blade angles

   2- the relative amount of diffusion or acceleration

   3- the energy transfer in case of rotor cascade (to/from the blade from/to the fluid i.e. turbine or compressor)

  4- losses or drage coefficient.

 

 

Effect of stagger angle on cascade performance.

A,B & C — compressor cascades.

D,E & F — turbine cascades.

 

Turbine reaction blading

 

 

     Fig. 4.9 Compressor blade forces (Without friction)

    

                                     

 

There is a pronounced increase in total pressure loss as the incidence rises beyond a certain value and the cascade is stalled in this region. The precise incidence at which stalling occurs is difficult to define and a stall point is arbitrarily specified as the incidence at which the total pressure loss is twice the minimum loss in total pressure. Physically, stall is characterised (at positive incidence) by the flow separating from the suction side of the blade surfaces. With decreasing incidence, total pressure losses again rise and a “negative incidence” stall point can also be defined as above. The working range is conventionally defined as the incidence range between these two limits at which the losses are twice the minimum loss. Accurate knowledge of the extent of the working range, obtained from two-dimensional cascade tests, is of great importance when attempting to assess the suitability of blading for changing conditions of operation.

A reference incidence angle can be most conveniently defined either at the midpoint of the working range or, less precisely, at the minimum loss condition. These two conditions do not necessarily give the same reference incidence.

5.7 HIGH-SPEED FLOWS

Many turbines and compressors experience flows at high Mach numbers. The high Mach number flow gives rise to some special problems which are characteristic of only high speed flows. Most of these problems arise due to the acceleration or deceleration (to subsonic Mach numbers) of supersonic flows in blade passages; expansion and compression waves are generated which affect the nature of flow and losses in these machines.

As stated before, when the Mach number reaches unity, the flow chokes and the maximum mass flow rate is governed by Eq. (5.82).

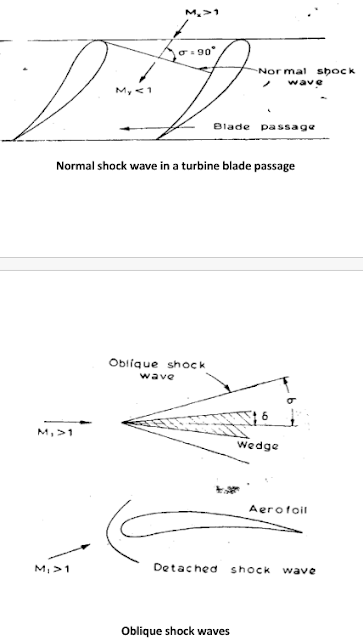
It is well known that in practice a supersonic flow decelerates to subsonic through a shock wave. This may be either normal or inclined to the direction of flow. In actual practice both the types of waves exist in supersonic machines.

The shock wave is an irreversibility and leads to stagnation pressure loss and increase in entropy.

 

 

HIGH-SPEED FLOWS

•        Many turbines and compressors experience flows at high Mach numbers.

•        The high Mach number flow gives rise to some special problems which are characteristic of only high speed flows.

•        Most of these problems arise due to the acceleration or deceleration (to subsonic Mach numbers) of supersonic flows in blade passages; expansion and compression waves are generated which affect the nature of flow and losses in these machines.

•        When the Mach number reaches unity, the flow chokes (there is a maximum mass flow rate which is indepentent the decrease of the downstream pressure).

HIGH-SPEED FLOWS (Continue)

•        It is well known that in practice a supersonic flow may decelerate to subsonic through a shock wave.

•        This may be either normal or inclined (oblique shocks) to the direction of flow. In actual practice both the types of waves exist in supersonic machines.

•        The shock wave is an irreversibility and leads to stagnation pressure loss and increase in entropy.

 

Normal shock wave in a turbine blade passage